张益唐被曝已证明黎曼猜想相关问题,震动数学(2)
此后,他多次提到过他正在关注这个问题。
这篇文章首次证明了距离有限的质数对是无穷多的,在孪生素数猜想这一数论难题上取得质的突破。
再后来,数学家也发展出了对应的解析工具来说明L函数在σ=1时无零点,从而证明了等差数列上的素数定理:
很明显,这个公式的限制条件要多了许多,所以大家当然希望L函数能够没有异常零点。
但这一个世纪以来的研究表明Landau-Siegel问题可能比黎曼猜想还要难解决。
1978至1985年,张益唐在北大数院拿到了本科和硕士学位,并在硕士期间师从我国著名数学家潘承彪。
至于具体证明了什么,还需要等待张益唐本人的正面回复了。
如果L函数所有的非平凡零点都落在这个区域内,就可以得到带余项的等差数列素数定理。
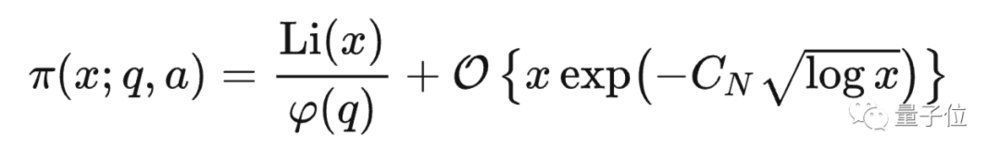
可惜的是,数学家Edmund Landau发现当X满足特殊性质时其对应的L函数可能会出现落在上面公式之外的异常零点(exceptional zero)。
而在这篇论文发表之前,他曾有令人羡慕的中外顶尖学府求学经历,但随后却经历了多年的蛰伏,甚至不得已跑去赛百味端盘子。
但这项工作的价值可以说是毋庸置疑,正如知乎网友爆料所述:
参考链接:
网传数学家张益唐,已经攻克了朗道-西格尔零点猜想(Landau-Siegel Zeros Conjecture)。
不过要说张益唐从默默无闻到名声大振,还得把时间的指针拨到2013年。
如此爆料,可谓是在数学界轰动不已。
不过需要说明的是,目前为止,张益唐本人并未在其他场合和形式宣布这一进展。
[5]https://weibo.com/2703634217/MatuJ2kAe?type=comment
曾有朋友向张益唐建议转行从事金融或计算机行业,但他并不愿意。
本文来自微信公众号:量子位 (ID:QbitAI),作者:金磊、Alex
End
[2]https://www.zhihu.com/question/559674941
因此,要是张益唐证明的是朗道-西格尔零点,那么黎曼猜想是错的。
这也就是为何大家都对这则消息都用“骇人听闻”来形容了。
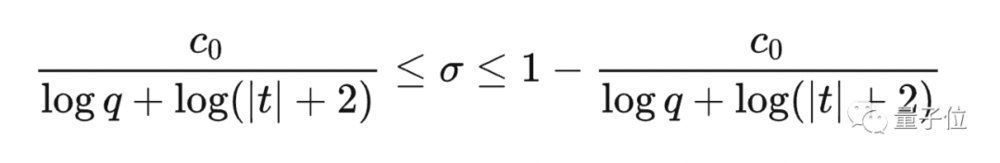
对它的证明,又为何会引发如此反响?
由于Landau和Siegel两位数学家在L函数异常零点这个领域里做了开创性的工作,所以异常零点也常常被称为Landau-Siegel零点。
在此期间,他曾到一位北大校友开的快餐连锁店赛百味担任会计。因为这样可以让他在工作中发挥记忆力和计算能力方面的特长,并抽空研究数学。
根据知乎博主“TravorLZH”的介绍,十九世纪的数学家为了研究素数分布引入了黎曼猜想。
那一年,他在数学最高期刊Annals of Mathematics上发表了震惊众多学者的《质数间的有界间隔》。
再加上他性格偏内向,以及在读博期间发表的学术论文太少等因素,竟没有任何一个美国大学或研究所愿意要他。
后来Walfisz利用这个更弱的非零区域得到了一个妥协版的等差数列素数定理:
整体来看,其实广义黎曼猜想恰好是Landau-Siegel猜想的充分条件。
而这则消息,据说是张益唐在参加北京大学校友Zoom线上会议时亲口所述。
文章来源:《应用数学》 网址: http://www.yysxzzs.cn/zonghexinwen/2022/1017/1684.html